Sketch-RNN でスケッチの自動生成（VAE + LSTM） - エクサウィザーズ Engineer Blog

こんにちは．エクサウィザーズでインターンをしている川畑です．

視覚によるコミュニケーションというのは人々が相手に何らかのアイデアを伝える際に鍵となります．私たちは小さい頃から物体を描く力を養ってきており，時には感情までもたった複数の線で表現することも可能です．こうした単純な絵というのは，身の回りのものを写真のように捉え忠実に再現したものではなく，どのようにして人間が物体の特徴を認識しそれらを再現するか，ということを教えてくれます．

そこで今回はSketch-RNNと呼ばれるRecurrent Neural Networkモデルでのスケッチの自動生成に取り組んでみました．このモデルは人間がするのと同じように抽象的な概念を一般化し，スケッチを生成することを目的としたものです．このモデルに関しては今の所具体的なアプリケーションが存在するというわけではなく，機械学習がどのようにクリエイティブな分野で活用できるか，という一例を提案したものになります．ソースコードはこちらからダウンロードできます．

f:id:k_kawabata:20181027163327p:plain [1] Google AI Blog: Teaching Machines to Draw

データセット

今回は論文でも用いられていたQuick, Draw!のデータセットを使用しました．これは20秒以内であるお題の絵を描くゲームで，データセットとしてネコやブタ，バスなど数百個のクラスのデータを公開しています．各クラスのデータは，訓練，検証，テストとしてそれぞれ70000，2500，2500のデータに分かれています．

Sketch-RNNモデルを学習させるにあたり，データのフォーマットとしては各点のデータが5つの要素からなるベクトル $\left(\Delta x, \Delta y, p_{1}, p_{2}, p_{3} \right)$ を使用しました．最初の二つの要素は，前の点からの $x, y$ の変位，残りの三つの要素はone-hotベクトルとなっています．一つ目のペン状態 $p_{1}$ はペンが現在紙に接していて，次の点まで線が描かれることを示しており，二つ目のペン状態 $p_{2}$ はそこでペンが紙から離れ，次の点まで線は引かれないことを示しており，三つ目のペン状態 $p_{3}$ はスケッチが終了することを示しています．

Sketch-RNNモデル

それではモデルについて解説していきたいと思います．

[2] A Neural Representation of Sketch Drawings

f:id:k_kawabata:20181027164205p:plain

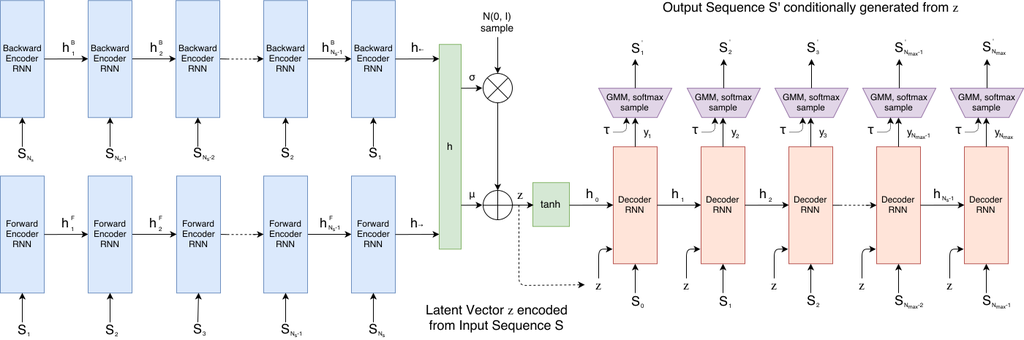
モデルの大枠はSequence-to-Sequence Variational Autoencoder (VAE) でできています．まず，エンコーダーであるbidirectional RNN (今回は単純なLSTMを使用)にスケッチのシーケンスを入力し，出力として潜在ベクトル $z$ を得ます．具体的には，双方向のRNNから得られた隠れ状態を連結し，全結合層によって連結された隠れ状態から $\mu$ および $\hat{\sigma}$ を得ます． $\hat{\sigma}$ に関しては，負にならないように $\sigma = \exp \left ({\frac{\hat{\sigma}}{2}} \right)$ の操作を加えます．そしてさらにガウス分布 $\mathcal{N}(0, I)$ と組み合わせることで最終的に潜在ベクトルを計算することができます．式で書くと以下のようになります．

$\displaystyle \mu = W_{\mu}h + b_{\mu}, \; \hat{\sigma} = W_{\sigma}h + b_{\sigma}, \; \sigma = \exp \left ({\frac{\hat{\sigma}}{2}} \right), \; z = \mu + \sigma\odot\mathcal{N}(0, I)$

潜在ベクトルが得られたら，次はデコーダーです．隠れ状態の初期値には潜在ベクトルに $tanh$ 関数を掛けたものを用います．

$\displaystyle \left[h_{0}; c_{0} \right] = tanh(W_{z}z + b_{z})$

各ステップでのデコーダーの入力には前ステップでのストローク $S_{i-1}$ と潜在ベクトル $z$ を連結したものを与え， $S_{0}$ にはスケッチの開始を意味する $(0, 0, 1, 0, 0)$ を与えるようにします．各ステップでの出力は次のデータ点の確率分布に関するパラメータを返します．Sketch-RNNでは $M$ 個の正規分布からなるGaussian mixture model (GMM)により $\left(\Delta x, \Delta y \right)$ を，カテゴリカル分布 $\left(q_{1}, q_{2}, q_{3} \right) \left(q_{1} + q_{2} + q_{3} = 1 \right)$ により真値である $\left(p_{1}, p_{2}, p_{3} \right)$ をモデル化します．

$\displaystyle p(\Delta x, \Delta y) = \sum_{j=1}^{M} \Pi _{j} \mathcal{N} \left(\Delta x, \Delta y \mid \mu_{x, j}, \mu_{y, j}, \sigma_{x, j}, \sigma_{y, j}, \rho_{xy, j} \right), where \sum_{j=1}^{M} \Pi_{j} = 1$

上の式において $\mathcal{N} \left(x, y \mid \mu_{x}, \mu_{y}, \sigma_{x}, \sigma_{y}, \rho_{xy} \right)$ は2変量正規分布を表しており，5つのパラメータ $\left(\mu_{x}, \mu_{y}, \sigma_{x}, \sigma_{y}, \rho_{xy} \right)$ で構成されます． $\mu_{x}, \mu_{y}$ は平均， $\sigma_{x}, \sigma_{y}$ は標準偏差， $\rho_{xy}$ は $x, y$ の相関係数です．また， $\Pi$ は長さ $M$ のベクトルであり，Gaussian mixture modelの各正規分布の重みに相当します．ですので，出力のサイズは3つのロジット $\left(q_{1}, q_{2}, q_{3} \right)$ も含めて合計で $5M + M + 3$ となります．

$\displaystyle x_{i} = \left[S_{i-1}; z \right], \left[h_{i}; c_{i} \right]$

$y_{i} = W_{y}h_{i} + b_{y}, \; y_{i} \in \mathbb{R}^{6M+3}$

ここで，出力ベクトル $y_{i}$ は次のように分解されます．

$\displaystyle \left[ (\hat{\Pi}_{1} \, \mu_{x} \, \mu_{y} \, \hat{\sigma}_{x} \, \hat{\sigma}_{y} \, \hat{\rho}_{xy})_{1} \ldots (\hat{\Pi}_{M} \, \mu_{x} \, \mu_{y} \, \hat{\sigma}_{x} \, \hat{\sigma}_{y} \, \hat{\rho}_{xy})_{M} \; (\hat{q}_{1} \, \hat{q}_{2} \, \hat{q}_{3}) \right] = y_{i}$

標準偏差，相関係数に関してはそれぞれ負にならないように，また-1から1の値を取るように $exp$ と $tanh$ による操作を施します．

$\displaystyle \sigma_{x} = \exp\left(\hat{\sigma}_{x} \right), \; \sigma_{y} = \exp\left(\hat{\sigma}_{y} \right), \; \rho_{xy} = tanh\left(\hat{\rho}_{xy} \right)$

カテゴリカル分布に関してはSoftmax関数を適応させ，全ての値が0〜1に収まるようにします．

$\displaystyle q_{k} = \frac{\exp(\hat{q}_{k})}{\sum_{j=1}^{3} \exp(\hat{q}_{j})}, \; k \in \{1, 2, 3\}, \; \Pi_{k} = \frac{\exp(\hat{\Pi}_{k})}{\sum_{j=1}^{M} \exp(\hat{\Pi}_{j})}, \; k \in \{1, \ldots , M\}$

損失関数

損失関数はVAEと同じでReconstruction Loss, $L_{R}$ とKullback-Leibler (KL) Divergence Loss, $L_{KL}$ の二つの項からなります．

Reconstruction Loss, $L_{R}$

Reconstruction Loss項は訓練データ $S$ を説明する確率分布の対数尤度を表しており，これを最大化するように学習します．そして，Reconstruction Loss, $L_{R}$ はさらに座標に関する項 $L_{s}$ とペン状態に関する項 $L_{p}$ からなっており，それぞれ以下のように書くことができます．

$\displaystyle L_{s} = -\frac{1}{N_{max}} \sum_{i=1}^{N_{s}}log \left(\sum_{j=1}^{M}\Pi_{j, i} \mathcal{N} \left(\Delta x_{i}, \Delta y_{i} \mid \mu_{x, j, i}, \mu_{y, j, i}, \sigma_{x, j, i}, \sigma_{y, j, i}, \rho_{xy, j, i} \right)\right)$

$\displaystyle L_{p} = -\frac{1}{N_{max}} \sum_{i=1}^{N_{max}} \sum_{k=1}^{3} p_{k, i} log\left(q_{k, i} \right)$

$L_{R} = L_{s} + L_{p}$

Kullback-Leibler (KL) Divergence Loss, $L_{KL}$

KL Divergence Loss項は潜在ベクトル $z$ が標準正規分布からどれだけ離れているかを表しており，これを最小化するように学習することになります．

$\displaystyle L_{KL} = -\frac{1}{2N_{z}} \left(1 + \hat{\sigma} - \mu^{2} - \exp(\hat{\sigma}) \right)$

実際に最適化する損失関数には $L_{R}$ と $L_{KL}$ を重み付けして足し合わせたものを用います．

$Loss = L_{R} + w_{KL}L_{KL}$

それぞれの損失項にはトレードオフの関係があり， $w_{KL} \rightarrow 0$ の時にはモデルは純粋なオートエンコーダーに近づき，より良いReconstruction Lossを得ることができる一方で，潜在空間における事前分布の強化を犠牲にすることになります．

サンプリング

モデルを学習させた後はいよいよスケッチの生成です．サンプリング過程では各ステップごとにGMMとカテゴリカル分布のパラメータを得，そのステップでの出力 $S_{i}'$ を得ます．訓練過程とは異なり，サンプリング過程では出力 $S_{i}'$ を次のステップの入力とし，このサンプリングステップを $p_{3} =1$ となるかステップ数が $N_{max}$ となるまで繰り返していきます．最終的に出力を得る際にはdeterministicに確率密度関数で最も確率の高い点を選ぶのではなく，下記のようにtemperatureパラメータ $\tau$ を導入することで出力のランダムさを調節できるようにしています． $\tau$ は0〜1の値を取り， $\tau = 0$ の時にはモデルはdeterministicになります．

$\displaystyle \hat{q}_{k} \rightarrow \frac{\hat{q}_{k}}{\tau}, \; \hat{\Pi}_{k} \rightarrow \frac{\hat{\Pi}_{k}}{\tau}, \; \sigma_{x}^{2} \rightarrow \sigma_{x}^{2}\tau, \; \sigma_{y}^{2} \rightarrow \sigma_{y}^{2}\tau$

コード

モデルに関する部分のコードを示します．Githubに論文著者によるオリジナルのコードもありますが，オリジナルではtensorflowで書かれていたものをkerasで書き換えました．全コードはこちらからダウンロードできます．

# below is where we need to do MDN (Mixture Density Network) splitting of
# distribution params
def get_mixture_coef(output, n_out):
  """Returns the tf slices containing mdn dist params."""
  # This uses eqns 18 -> 23 of http://arxiv.org/abs/1308.0850.
  z = output
  z = tf.reshape(z, [-1, n_out])
  z_pen_logits = z[:, 0:3]  # pen states
  z_pi, z_mu1, z_mu2, z_sigma1, z_sigma2, z_corr = tf.split(z[:, 3:], 6, 1)

  # process output z's into MDN paramters

  # softmax all the pi's and pen states:
  z_pi = tf.nn.softmax(z_pi)
  z_pen = tf.nn.softmax(z_pen_logits)

  # exponentiate the sigmas and also make corr between -1 and 1.
  z_sigma1 = K.exp(z_sigma1)
  z_sigma2 = K.exp(z_sigma2)
  z_corr = tf.tanh(z_corr)

  r = [z_pi, z_mu1, z_mu2, z_sigma1, z_sigma2, z_corr, z_pen, z_pen_logits]
  return r


class SketchRNN():
  """SketchRNN model definition."""

  def __init__(self, hps):
    self.hps = hps # hps is hyper parameters
    self.build_model(hps)

  def build_model(self, hps):
    # VAE model = encoder + Decoder
    # build encoder model
    encoder_inputs = Input(shape=(hps.max_seq_len, 5), name='encoder_input')
    # (batch_size, max_seq_len, 5)
    encoder_lstm = LSTM(hps.enc_rnn_size,
                use_bias=True,
                recurrent_initializer='orthogonal',
                bias_initializer='zeros',
                recurrent_dropout=1.0-hps.recurrent_dropout_prob,
                return_sequences=True,
                return_state=True)
    bidirectional = Bidirectional(encoder_lstm)
    (unused_outputs, # (batch_size, max_seq_len, enc_rnn_size * 2)
    last_h_fw, unused_c_fw, # (batch_size, enc_rnn_size) * 2
    last_h_bw, unused_c_bw) = bidirectional(encoder_inputs)
    last_h = concatenate([last_h_fw, last_h_bw], 1)
    # (batch_size, enc_rnn_size*2)

    normal_init = RandomNormal(stddev=0.001)
    self.z_mean = Dense(hps.z_size,
                  activation='linear',
                  use_bias=True,
                  kernel_initializer=normal_init,
                  bias_initializer='zeros')(last_h) # (batch_size, z_size)
    self.z_presig = Dense(hps.z_size,
                  activation='linear',
                  use_bias=True,
                  kernel_initializer=normal_init,
                  bias_initializer='zeros')(last_h) # (batch_size, z_size)

    def sampling(args):
      z_mean, z_presig = args
      self.sigma = K.exp(0.5 * z_presig)
      batch = K.shape(z_mean)[0]
      dim = K.int_shape(z_mean)[1]
      epsilon = K.random_normal((batch, dim), 0.0, 1.0)
      batch_z = z_mean + self.sigma * epsilon

      return batch_z # (batch_size, z_size)

    self.batch_z = Lambda(sampling,
                    output_shape=(hps.z_size,))([self.z_mean, self.z_presig])

    # instantiate encoder model
    self.encoder = Model(
                    encoder_inputs,
                    [self.z_mean, self.z_presig, self.batch_z], name='encoder')
    # self.encoder.summary()

    # build decoder model
    # Number of outputs is 3 (one logit per pen state) plus 6 per mixture
    # component: mean_x, stdev_x, mean_y, stdev_y, correlation_xy, and the
    # mixture weight/probability (Pi_k)
    self.n_out = (3 + hps.num_mixture * 6)

    decoder_inputs = Input(shape=(hps.max_seq_len, 5), name='decoder_input')
    # (batch_size, max_seq_len, 5)
    overlay_x = RepeatVector(hps.max_seq_len)(self.batch_z)
    # (batch_size, max_seq_len, z_size)
    actual_input_x = concatenate([decoder_inputs, overlay_x], 2)
    # (batch_size, max_seq_len, 5 + z_size)

    self.initial_state_layer = Dense(hps.dec_rnn_size * 2,
            activation='tanh',
            use_bias=True,
            kernel_initializer=normal_init)
    initial_state = self.initial_state_layer(self.batch_z)
    # (batch_size, dec_rnn_size * 2)
    initial_h, initial_c = tf.split(initial_state, 2, 1)
    # (batch_size, dec_rnn_size), (batch_size, dec_rnn_size)
    self.decoder_lstm = LSTM(hps.dec_rnn_size,
            use_bias=True,
            recurrent_initializer='orthogonal',
            bias_initializer='zeros',
            recurrent_dropout=1.0-hps.recurrent_dropout_prob,
            return_sequences=True,
            return_state=True
            )

    output, last_h, last_c = self.decoder_lstm(
                          actual_input_x, initial_state=[initial_h, initial_c])
    # [(batch_size, max_seq_len, dec_rnn_size), ((batch_size, dec_rnn_size)*2)]
    self.output_layer = Dense(self.n_out, activation='linear', use_bias=True)
    output = self.output_layer(output)
    # (batch_size, max_seq_len, n_out)

    last_state = [last_h, last_c]
    self.final_state = last_state

    # instantiate SketchRNN model
    self.sketch_rnn_model = Model(
                  [encoder_inputs, decoder_inputs],
                  output,
                  name='sketch_rnn')
    # self.sketch_rnn_model.summary()

  def vae_loss(self, inputs, outputs):
    # KL loss
    kl_loss = 1 + self.z_presig - K.square(self.z_mean) - K.exp(self.z_presig)
    self.kl_loss = -0.5 * K.mean(K.sum(kl_loss, axis=-1))
    self.kl_loss = K.maximum(self.kl_loss, K.constant(self.hps.kl_tolerance))

    # the below are inner functions, not methods of Model
    def tf_2d_normal(x1, x2, mu1, mu2, s1, s2, rho):
      """Returns result of eq # 24 of http://arxiv.org/abs/1308.0850."""
      norm1 = subtract([x1, mu1])
      norm2 = subtract([x2, mu2])
      s1s2 = multiply([s1, s2])
      # eq 25
      z = (K.square(tf.divide(norm1, s1)) + K.square(tf.divide(norm2, s2)) -
           2 * tf.divide(multiply([rho, multiply([norm1, norm2])]), s1s2))
      neg_rho = 1 - K.square(rho)
      result = K.exp(tf.divide(-z, 2 * neg_rho))
      denom = 2 * np.pi * multiply([s1s2, K.sqrt(neg_rho)])
      result = tf.divide(result, denom)
      return result

    def get_lossfunc(z_pi, z_mu1, z_mu2, z_sigma1, z_sigma2, z_corr,
                     z_pen_logits, x1_data, x2_data, pen_data):
      """Returns a loss fn based on eq #26 of http://arxiv.org/abs/1308.0850."""
      # This represents the L_R only (i.e. does not include the KL loss term).

      result0 = tf_2d_normal(x1_data, x2_data, z_mu1, z_mu2, z_sigma1, z_sigma2,
                             z_corr)
      epsilon = 1e-6
      # result1 is the loss wrt pen offset (L_s in equation 9 of
      # https://arxiv.org/pdf/1704.03477.pdf)
      result1 = multiply([result0, z_pi])
      result1 = K.sum(result1, 1, keepdims=True)
      result1 = -K.log(result1 + epsilon)  # avoid log(0)

      fs = 1.0 - pen_data[:, 2]  # use training data for this
      fs = tf.reshape(fs, [-1, 1])
      # Zero out loss terms beyond N_s, the last actual stroke
      result1 = multiply([result1, fs])

      # result2: loss wrt pen state, (L_p in equation 9)
      result2 = tf.nn.softmax_cross_entropy_with_logits_v2(
                        labels=pen_data, logits=z_pen_logits)
      result2 = tf.reshape(result2, [-1, 1])
      result2 = multiply([result2, fs])

      result = result1 + result2
      return result

    # reshape target data so that it is compatible with prediction shape
    target = tf.reshape(inputs, [-1, 5])
    [x1_data, x2_data, eos_data, eoc_data, cont_data] = tf.split(target, 5, 1)
    pen_data = concatenate([eos_data, eoc_data, cont_data], 1)

    out = get_mixture_coef(outputs, self.n_out)
    [o_pi, o_mu1, o_mu2, o_sigma1, o_sigma2, o_corr, o_pen, o_pen_logits] = out

    lossfunc = get_lossfunc(o_pi, o_mu1, o_mu2, o_sigma1, o_sigma2, o_corr,
                            o_pen_logits, x1_data, x2_data, pen_data)

    self.r_loss = tf.reduce_mean(lossfunc)

    kl_weight = self.hps.kl_weight_start
    self.loss = self.r_loss + self.kl_loss * kl_weight
    return self.loss

  def model_compile(self, model):
      adam = Adam(lr=self.hps.learning_rate, clipvalue=self.hps.grad_clip)
      model.compile(loss=self.vae_loss, optimizer=adam)

以下は学習後のモデルからスケッチを生成するサンプリングのコードです．

def sample(model, hps, weights, seq_len=250, temperature=1.0,
            greedy_mode=False, z=None):
  """Samples a sequence from a pre-trained model."""

  def adjust_temp(pi_pdf, temp):
    pi_pdf = np.log(pi_pdf) / temp
    pi_pdf -= pi_pdf.max()
    pi_pdf = np.exp(pi_pdf)
    pi_pdf /=pi_pdf.sum()
    return pi_pdf

  def get_pi_idx(x, pdf, temp=1.0, greedy=False):
    """Samples from a pdf, optionally greedily."""
    if greedy:
      return np.argmax(pdf)
    pdf = adjust_temp(np.copy(pdf), temp)
    accumulate = 0
    for i in range(0, pdf.size):
      accumulate += pdf[i]
      if accumulate >= x:
        return i
    tf.logging.info('Error with smpling ensemble.')
    return -1

  def sample_gaussian_2d(mu1, mu2, s1, s2, rho, temp=1.0, greedy=False):
    if greedy:
      return mu1, mu2
    mean = [mu1, mu2]
    s1 *= temp * temp
    s2 *= temp * temp
    cov = [[s1 * s1, rho * s1 * s2], [rho * s1 * s2, s2 * s2]]
    x = np.random.multivariate_normal(mean, cov, 1)
    return x[0][0], x[0][1]

  # load model
  model.sketch_rnn_model.load_weights(weights)

  prev_x = np.zeros((1, 1, 5), dtype=np.float32)
  prev_x[0, 0, 2] = 1 # initially, we want to see beginning of new stroke
  if z is None:
    z = np.random.randn(1, hps.z_size)

  batch_z = Input(shape=(hps.z_size,)) # (1, z_size)
  initial_state = model.initial_state_layer(batch_z)
  # (1, dec_rnn_size * 2)

  decoder_input = Input(shape=(1, 5)) # (1, 1, 5)
  overlay_x = RepeatVector(1)(batch_z) # (1,1, z_size)
  actual_input_x = concatenate([decoder_input, overlay_x], 2)
  # (1, 1, 5 + z_size)

  decoder_h_input = Input(shape=(hps.dec_rnn_size, ))
  decoder_c_input = Input(shape=(hps.dec_rnn_size, ))
  output, last_h, last_c = model.decoder_lstm(
                        actual_input_x,
                        initial_state=[decoder_h_input, decoder_c_input])
  # [(1, 1, dec_rnn_size), (1, dec_rnn_size), (1, dec_rnn_size)]
  output = model.output_layer(output)
  # (1, 1, n_out)

  decoder_initial_model = Model(batch_z, initial_state)
  decoder_model = Model([decoder_input, batch_z,
                        decoder_h_input, decoder_c_input],
                        [output, last_h, last_c])

  prev_state = decoder_initial_model.predict(z)
  prev_h, prev_c = np.split(prev_state, 2, 1)
  # (1, dec_rnn_size), (1, dec_rnn_size)

  strokes = np.zeros((seq_len, 5), dtype=np.float32)
  greedy = False
  temp =  1.0

  for i in range(seq_len):
    decoder_output, next_h, next_c = decoder_model.predict(
                                          [prev_x, z, prev_h, prev_c])
    out = sketch_rnn_model.get_mixture_coef(decoder_output, model.n_out)
    [o_pi, o_mu1, o_mu2, o_sigma1, o_sigma2, o_corr, o_pen, o_pen_logits] = out

    o_pi = K.eval(o_pi)
    o_mu1 = K.eval(o_mu1)
    o_mu2 = K.eval(o_mu2)
    o_sigma1 = K.eval(o_sigma1)
    o_sigma2 = K.eval(o_sigma2)
    o_corr = K.eval(o_corr)
    o_pen = K.eval(o_pen)

    if i < 0:
      greedy = False
      temp = 1.0
    else:
      greedy = greedy_mode
      temp = temperature

    idx = get_pi_idx(random.random(), o_pi[0], temp, greedy)

    idx_eos = get_pi_idx(random.random(), o_pen[0], temp, greedy)
    eos=[0, 0, 0]
    eos[idx_eos] = 1

    next_x1, next_x2 = sample_gaussian_2d(o_mu1[0][idx], o_mu2[0][idx],
                                          o_sigma1[0][idx], o_sigma2[0][idx],
                                          o_corr[0][idx], np.sqrt(temp), greedy)

    strokes[i, :] = [next_x1, next_x2, eos[0], eos[1], eos[2]]

    prev_x = np.zeros((1, 1, 5), dtype=np.float32)
    prev_x[0][0] = np.array(
        [next_x1, next_x2, eos[0], eos[1], eos[2]], dtype=np.float32)
    prev_h, prev_c = next_h, next_c

  # delete model to avoid a memory leak
  K.clear_session()

  return strokes

結果

今回は時間の都合上フクロウのデータセットでのみモデルの学習を行いました．それではまず入力に用いるスケッチをテストセットからランダムに選んできて，どのようなスケッチか見てみましょう．ちなみにこれは人間がフクロウを描いたものです．

f:id:k_kawabata:20181029021841p:plain

正直フクロウっぽくないですが一応生き物っぽいので良しとします．

次にこのスケッチからエンコーダーによって潜在ベクトルを得ます．

f:id:k_kawabata:20181029022225p:plain

そして最後にデコーダーによってスケッチを生成します．

f:id:k_kawabata:20181029022427p:plain

なかなかフクロウっぽいのではないでしょうか？

それでは次に様々なtemperatureパラメータを用いた時にスケッチがどのように変化していくか見ていきましょう．

f:id:k_kawabata:20181029022849p:plain

右にいくほどtemperatureの値は大きくなります．つまり，よりランダムになっていきます．temperatureが0.1の時はどちらかと言うとペンギンぽいですが，temperatureが0.3と0.5の時はかなりフクロウっぽいスケッチになっています．

かなり荒削りな部分もありますが，スケッチとして認識できるレベルまでしっかり学習ができていることがわかります．ただ，一つ気になったこととしては入力画像にかかわらず常にペンギンのようなスケッチを生成してしまっていたことです．ここの例でも示している通り，入力をかなり無視してペンギンのようなスケッチを生成しています．論文著者のコードではRNNセルにLayer Normalization付きのLSTMやHyperLSTMを用いることができるようになっており，またKL Lossのアニーリングも行なっていたのですが今回の実装ではそれらは含まれていなかったためこのような結果になったのではないかと考えています．入力画像に関係なく毎回同じようなスケッチを生成することに関しては，特にKL Lossのアニーリングを行なっていないことで，Reconstruction Lossに比べてKL Lossにばかり重点が置かれたことが原因だと考えています．

参照

最後に

尚，エクサウィザーズは20卒向けのAIエンジニアのポジションで，内定直結型インターンを東京・京都オフィスで募集しています．ご興味を持たれた方はぜひご応募ください．

ご応募はこちらから