因果推論とグラフ理論 - エクサウィザーズ Engineer Blog

こんにちは。数理最適化ギルドでエンジニアをしている加藤です。

ある自社プロダクトの開発を通じて因果推論について勉強する機会がありました。因果推論は統計の分野ですが、その中で数理最適化の技術が使えることを知り、とても面白かったのでその内容をシェアしようと思います。具体的には組合せ最適化問題のひとつである最小カット問題が、因果推論のタスクの一部である識別可能性に利用できるという話をします。

前半は因果推論についての概説で特に予備知識は仮定していないです。後半は計算時間やネットワークフローなどのアルゴリズムを知っていると読みやすいと思います。

因果推論とは

因果推論の目的

統計的因果推論とは事象の間の因果効果を実験データや観測データから推定することを目的とした統計学の一分野です。単に因果推論といった場合は統計的因果推論を含むより広い概念を指すことがありますが、簡単のため以下では因果推論といえば統計的因果推論のことであるとします。

例えばある販促キャンペーンを実施したときに、本当に効果があったのかどうかなどを合理的に判断することなどに利用できます。この例のように物事の原因となったと想定されるものを処置（トリートメント）変数、その原因に影響を受けたと想定されるものを結果（成果・アウトカム）変数と言います。また処置が結果に与えた影響の大きさを因果効果と言います。

因果推論には主にRubin流の潜在的アウトカムを用いる流儀とPearl流の因果グラフを用いる流儀があります。本稿で説明するのは後者のPearl流因果推論です。

因果関係があるどうかを判断するというのは意外と難しく、その理由の一つは人間は相関関係を因果関係を誤認してしまうことにあります。

因果≠相関

相関・因果の誤謬の例としてしばしば引き合いに出されるのが次のグラフです[1]。

これは一流の医学雑誌に掲載された論文の分析で「一人当たりのチョコレートの年間消費量が多い国ほどノーベル賞受賞者が多い」という相関関係がわかります。論文の著者は「国民が1人あたり年間400ｇ多くチョコレートを摂取すると、その国のノーベル賞受賞者の数が1人増える」と結論づけていますがこれは当然正しい推論ではなく、実際は「一人当たりGDP」という変数が前者と後者の変数どちらには影響を与えることによって生み出されている擬似的な相関です。疑似的な相関（あるいは疑似的な無相関）のことを交絡といい、交絡を作り出すの「一人当たりGDP」のような変数を交絡変数と呼びます。こういった擬似相関を排除したい場合はどうすれば良いのでしょうか？

もう少し単純な例で考えてみます。次の表をご覧ください。

この表は何かしらの疾病・怪我などに対して治療した場合としなかった場合での生存・死亡数を表しています。治療をした場合もしなかった場合も生存率が50%で変わっていないので一見この治療には効果がないように見えます。しかし次の表を見てください。

この表をみると男性を治療した場合の生存率は約62%、しなかった場合は約57%なので治療によって生存率が上がっています。一方女性も治療した場合が約44%、しなかった場合が40%なのでこちらも生存率が上がっています。つまり一見効果がないように見えた治療でしたが、男女別にすると治療効果が見えてくるということがあります。

このように層別化などによって正しい因果効果が推定できるような変数の集合のことを調整変数と呼びます。また調整変数が観測できるとき因果効果は識別可能であると言います。つまり上の例では「チョコレート消費量→ノーベル賞受賞者数」の因果効果を正しく推定するための調整変数が「一人当たりGDP」なので、この因果効果は識別可能であるということになります。

調整変数選択の難しさ

調整変数によって層別化すれば正しい因果効果を推定できると述べましたが、肝心の調整変数はどうやって選択すれば良いのでしょうか？少なくともなんでもかんでも調整変数に含めれば良いわけではないということが次の例でわかります。次の表を見てください。

この表は幼児が遊んだトランプの分類です。数値的には先ほどの表と全く同じです。汚れありのグループをみると絵札より数札の方が赤札の割合が高いです。一方汚れなしのグループも絵札より数札の方が赤札の割合が高いです。つまり「汚れの有無にかかわらず、絵札より数札の方が赤札の割合が高い」と読めます。しかし絵札も数札も赤と黒は同数あるので「絵札より数札の方が赤札の割合が高い」という主張は当然正しくありません。したがってこの例では「汚れの有無」という属性で分けることで間違った結論を導いてしまいます。

上記の例のように層別化することでバイアスが発生してしまうことを選択バイアスと呼びます。*1

このように何を調整変数にすべきか・そもそも調整変数は存在するのか（識別可能どうか）を判断するのは難しい問題ですが、その問いへの回答として冒頭でも触れたPearlの因果グラフの理論があります。続く記事ではその内容を解説します。

因果グラフ

グラフとは

グラフとは物事のつながりを表現するための構造のひとつです。現実世界のさまざまなものをモデル化する力があり、因果推論以外の文脈でも頻繁に現れる対象です。

数学的にはノードとエッジと呼ばれる対象から構成され、ノードはグラフの頂点でエッジはふたつのノードをつなぐ辺を意味します。フォーマルな定義は以下です。ついでに後々使う概念の定義もしておきます。

定義（グラフ） $G = (V, E)$ をグラフという。 $V$ の要素をノードあるいは頂点という。 $E$ は $V$ の要素のペアからなる集合で、その要素をエッジあるいは辺という。エッジに向きが指定されている場合そのエッジは向きがついているという。また $U$ から $V$ への向きがついたエッジは $U \to V$ と書く。また $U$ をエッジの始点、 $V$ をエッジの終点という。

定義（無向グラフ、有向グラフ、単純グラフ）全てのエッジに向きが付いているグラフを有向グラフという。逆に全てのエッジに向きがついていないグラフを無向グラフという。全てのノードのペアに対して高々一つしか辺がなく、全てのノードが自分自身へのエッジを持たないグラフを単純グラフという。以後グラフは全て単純であるとする。

定義（パス、ループ）ノードの列 $N_0, N_1, \cdots, N_p$ であって全ての $i$ に対して $N_i$ と $N_{i + 1}$ の間にエッジが存在するものをパスという。またそれらが全て $N_i$ から $N_{i + 1}$ へ向きがついている場合、このパスを有向パスという。また $N_0$ および $N_p$ をそれぞれパスの始点および終点という。始点と終点が一致しているパスをループと呼び、それが有向パスである場合に有効ループと呼ぶ。

定義（親、祖先、子、子孫）有向グラフのノード $N$ に対して $N$ に入ってくるエッジの始点であるノードを $N$ の親、 $N$ から出ていくノードの終点であるノードを子、 $N$ を終点とする有向パスの始点を祖先、 $N$ を終点とする有向パスの終点を子孫という。

定義（DAG）単純な有向グラフであって有向ループを持たないものをDAG（有効非巡回グラフ）という。

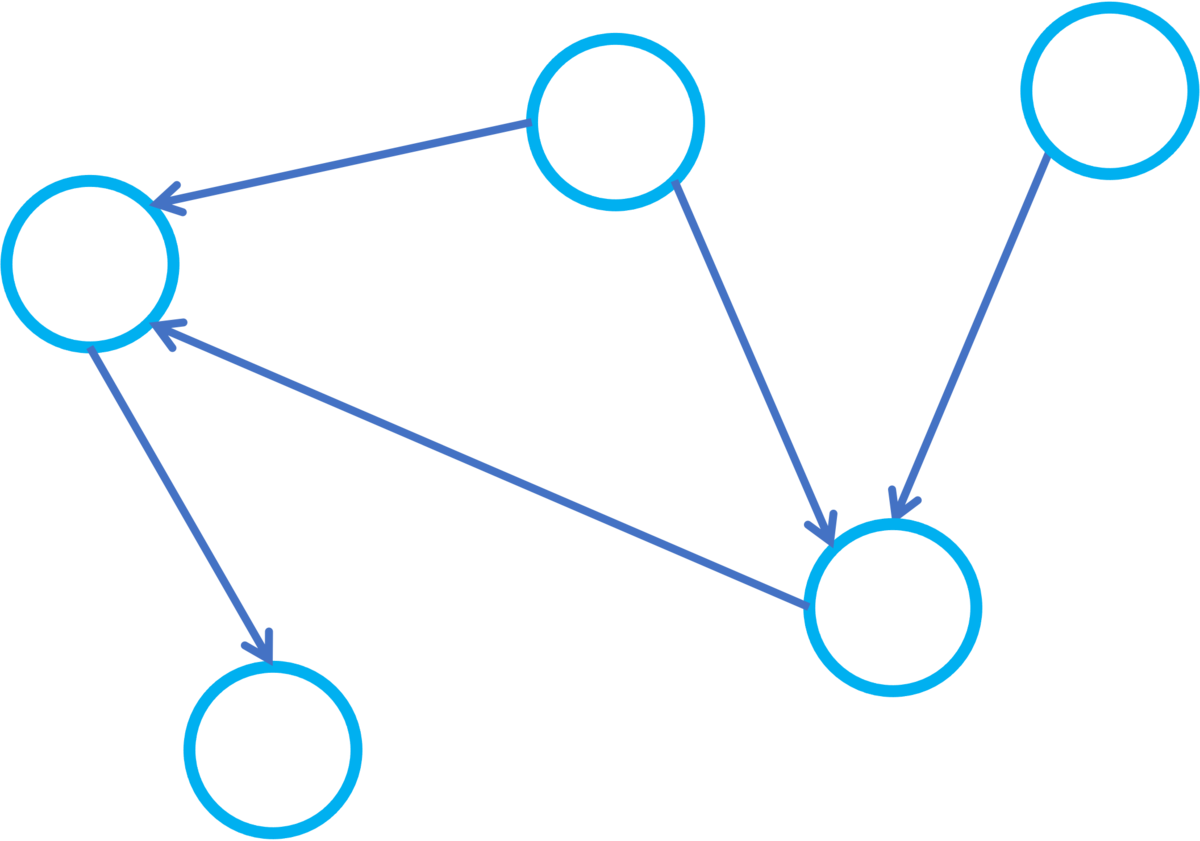
因果推論においてはノードに事象あるいは変数を対応させ、エッジは因果関係を表します。このように因果関係をグラフで表現したものを因果グラフと呼びます。また因果グラフ上でノード $U$ からノード $V$ にエッジが存在するとき $U$ は $V$ の原因であるということがあります。

交絡の例

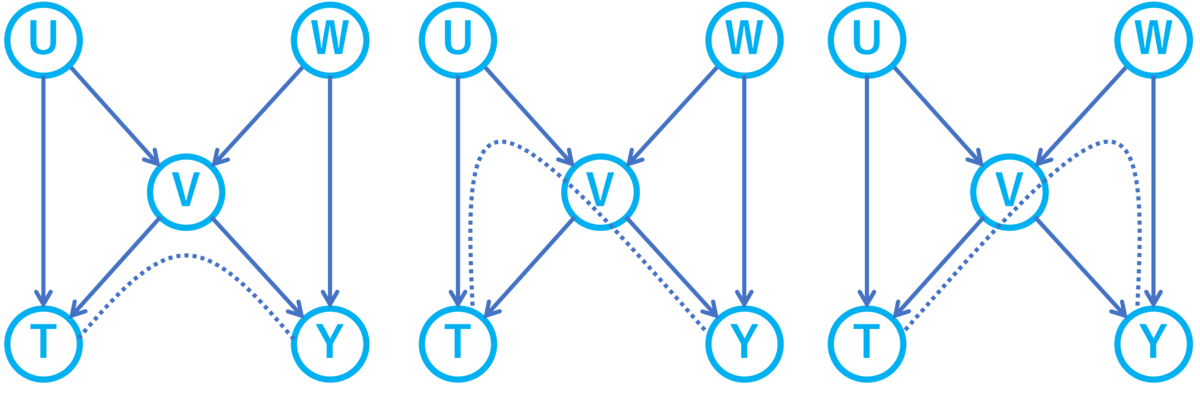
因果グラフを使うと交絡変数は次のように表せます。ただしT, Y, Uがそれぞれ処置変数、結果変数、交絡変数を表します。以下で矢印の実線は因果関係を、波線は交絡を表していると考えてください。

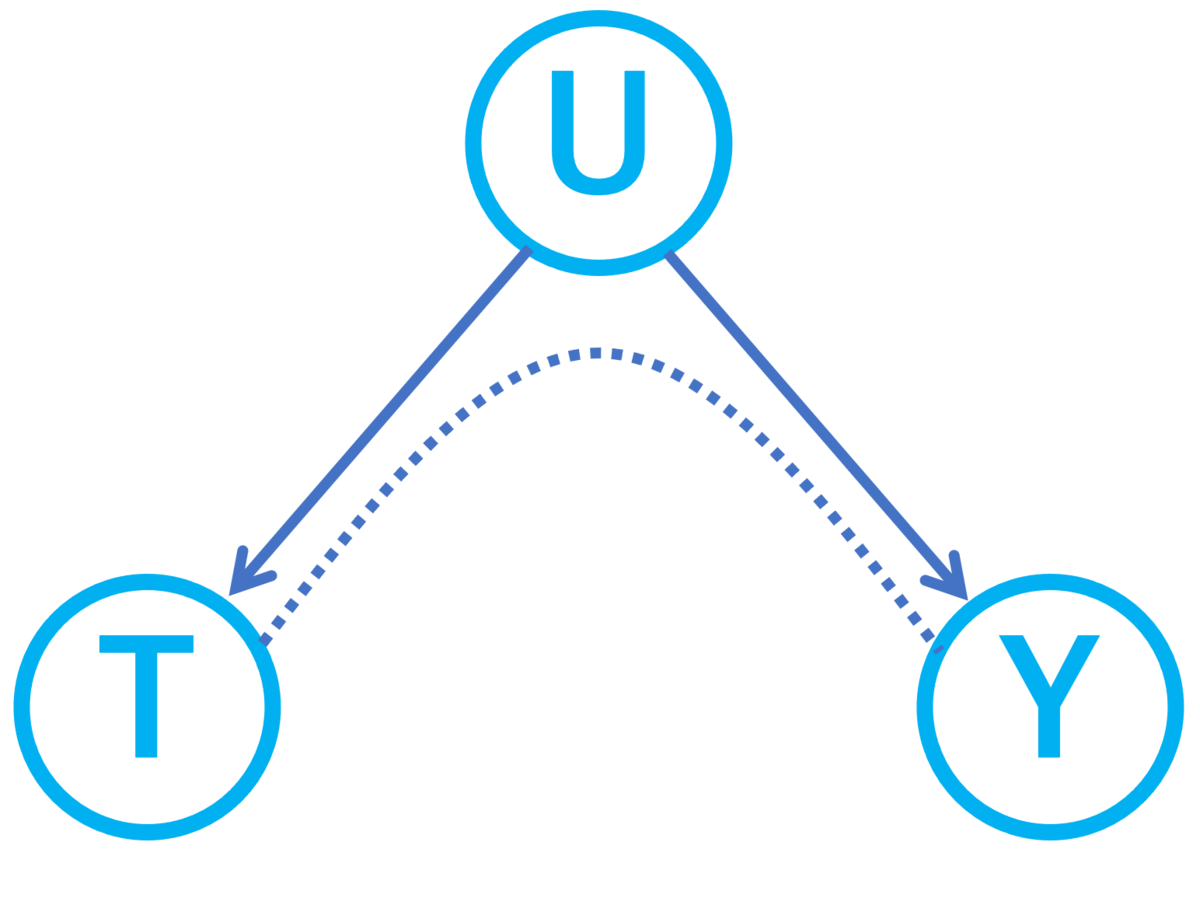
交絡変数Uで調整することにより交絡を取り除く様子を次のように表現します。

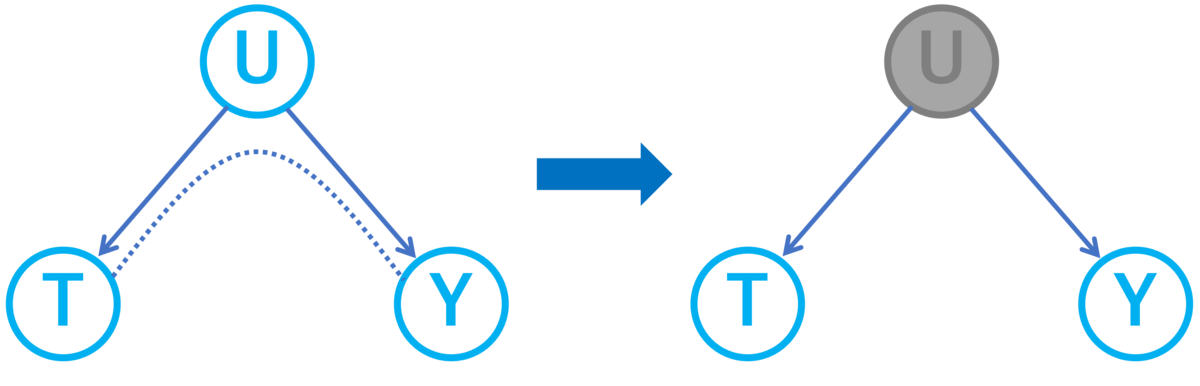
逆に調整変数にすべきでない変数による交絡が生じる場合もあります。以下のように調整変数も結果変数も原因であるような変数で調整すると選択バイアスによる交絡が生まれます。

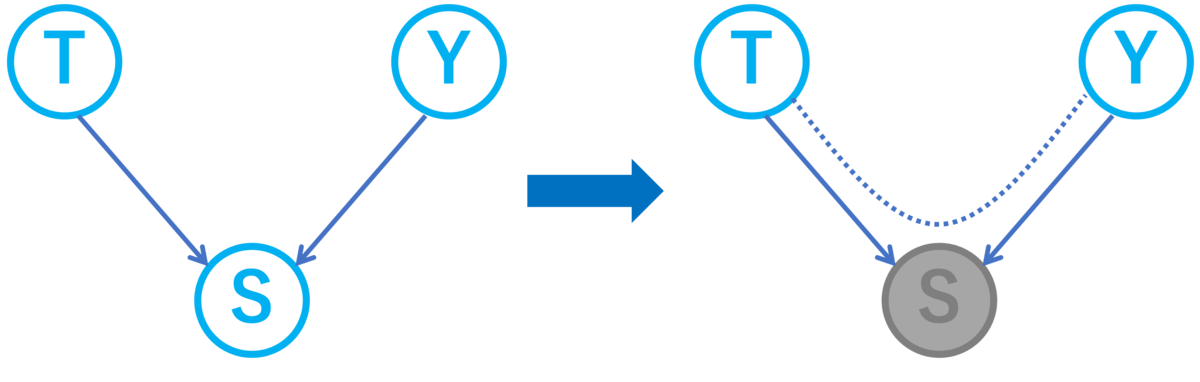
このように因果関係をグラフによって表現し、交絡変数や選択バイアスを視覚的に表現できます。もう少し複雑な例を考えてみましょう。次のグラフをご覧ください。

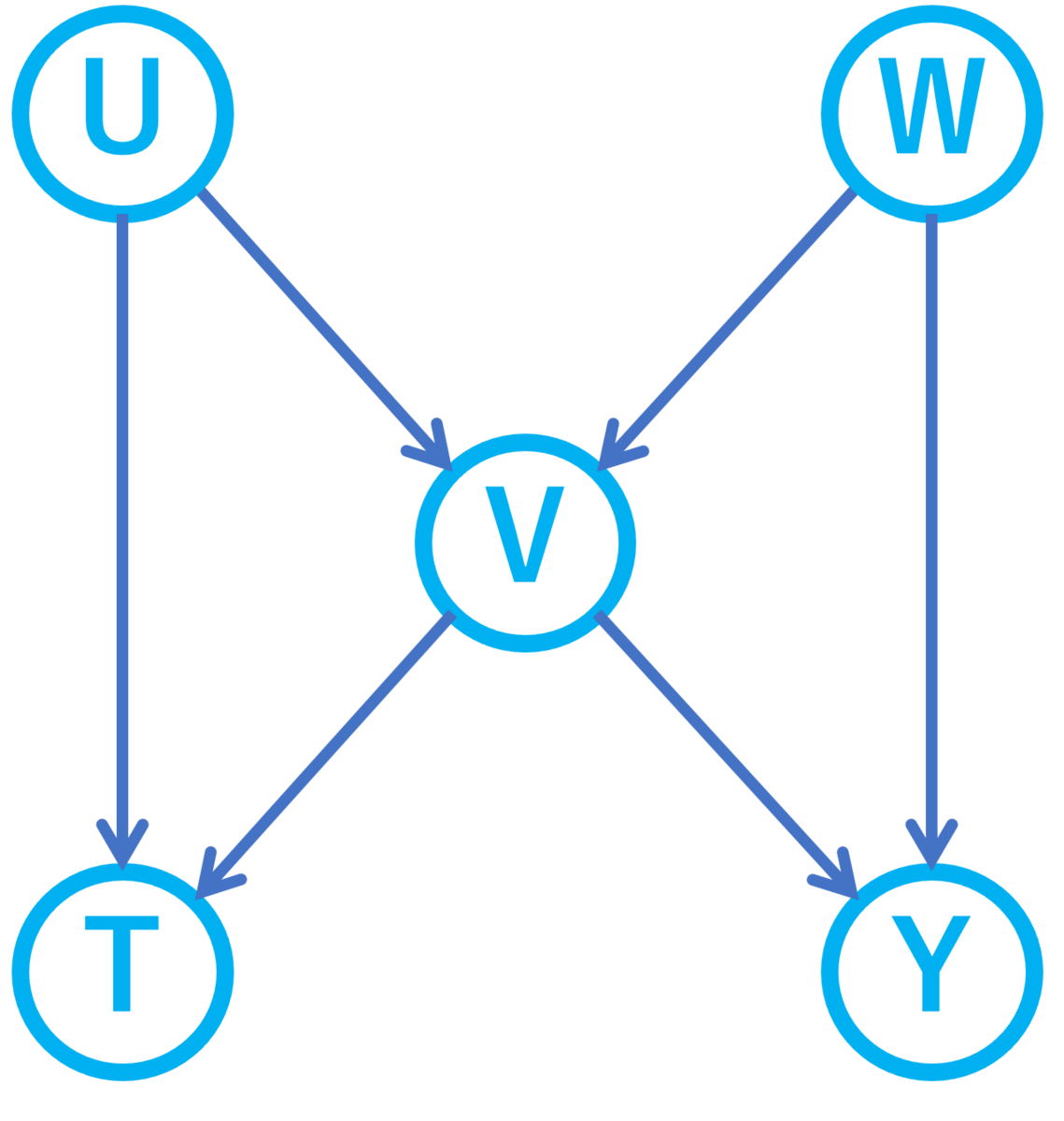
上記の例ではまず $V$ が交絡変数になっています。また $U$ が $T$ と $V$ の交絡因子になっており、 $V$ が $Y$ の原因なので $T \gets U \to V \to Y$ というパスを介して $T$ と $Y$ は関係しあっています。同様に $T \gets V \gets W \to Y$ というパスもありこれも $T$ と $Y$ の交絡を作り出しています。このような処置変数 $T$ に入ってくるエッジからスタートする結果変数 $Y$ へのパスをバックドアパスと呼びます。

これらの交絡を取り除くためにはどのような調整変数を選択すれば良いでしょうか。実は $V$ を調整変数にすると上記３つの交絡は全て取り除けます。なぜなら上記３つの交絡をもたらすバックドアパスの経路上に $V$ が存在して交絡をブロックしているためです。バックドアパスとパスのブロックのフォーマルな定義は以下になります。

定義（バックドアパス）有向グラフ $G = (V, E)$ の頂点 $T, Y \in V$ に対して $T$ から $Y$ への有向とは限らないパスであって $T$ へ入ってくるエッジからスタートするものをバックドアパスという。

定義（パスのブロック）有向グラフ $G = (V, E)$ とその頂点の部分集合 $S \subset V$ および $G$ 上の有向とは限らないパス $\gamma$ が次のいずれかの条件を満たすとき $S$ は $\gamma$ をブロックするという。

1. $\gamma$ 上の合流点であって、自分を含む全ての子孫が $S$ に含まれないものが存在する。 2. $\gamma$ 上の非合流点であって $S$ に含まれるものが存在する。

ただしパス上の端点以外のノードであってパス上で隣り合う二点からエッジが入ってくるようなノードを合流点と呼んでいる。

しかし一方で別の問題が発生します。それは $V$ を調整変数にすることで $U \to V \gets W$ に選択バイアスが生まれ $T \gets U \to V \gets W \to Y$ という新たな交絡が生じてしまうのです。この新たな交絡を取り除くためには ${U, V}$ などを調整変数として選ぶ必要があります。

上のような特殊な例に限らず交絡を取り除くためにはどんな調整変数を選べば良いのでしょうか。その答えが次のd分離性です。

定義（d分離）有向グラフ $G = (V, E)$ の頂点 $T, Y \in V$ と頂点の部分集合 $S \subset V$ が次の性質を満たすとき $S$ は $\{T, Y\}$ をd分離（有効分離）するという。 $T$ から $Y$ への全ての有向とは限らないパス $\gamma$ に対して $S$ は $\gamma$ をブロックする。

少し面倒ですが上述の特殊な例において $\{U, V\}$ が $\{T, Y\}$ をd分離していることが確認できます。

有効分離があるのに無向分離はないのかと思われるかも知れませんが一応こちらもあります。後で使うのでここで定義しておきます。

定義（u分離）有向グラフ $G = (V, E)$ の頂点 $T, Y \in V$ と頂点の部分集合 $S \subset V$ が次の性質を満たすとき $S$ は $\{T, Y\}$ をu分離（無向分離）するという。 $T$ から $Y$ への全ての（無向）パス $\gamma$ に対して $\gamma$ 上に $S$ の要素が少なくとも１つ存在する。

バックドア基準

さらに一歩進んでバックドア基準についても述べておきます。交絡を取り除いて因果効果のみを知りたいときに有用な概念です。

定義（バックドア基準）因果グラフ $G = (V, E)$ とそのふたつの頂点 $T, Y \in V$ に対して次の条件を満たすノードの集合 $S \subset V$ をバックドア基準を満たすという。

すべてのノード $Z \in S$ に対して $T$ から $Z$ への有向パスが存在しない。
$\{T, Y\} \cup S$ の祖先グラフ上で $S$ は $T$ と $Y$ をd分離する。

ただし有向グラフ $G = (V, E)$ のノードの集合 $V_0 \subset V$ に対してその祖先グラフとは、ノード $V^{an}$ を $V_0$ のすべての要素およびその祖先とし、エッジ $E^{an}$ を $G$ のエッジであってその始点・終点が $V^{an}$ の要素であるものとするグラフのことである。

やや定義が複雑ですがバックドア基準を満たす変数集合を調整変数として選べば介入効果などが表現できることが知られています[2]。

ところで処置変数の親を全て調整変数にすれば必ずバックドア基準を満たすことも知られています。しかしこれは必ずしも良い選択ではありません。調整変数は層別化や回帰といった用途に用いられる変数なので、できるだけ少ない数の調整変数が知りたいという欲求があります。

つまり我々の目標は次のようになります

バックドア基準を満たす最小の変数集合を見つけたい！

定義よりバックドア基準はd分離性と密接に関わっていることがわかると思いますので次のような目標設定でも良いです。

d分離性を満たす最小の変数集合を見つけたい！

次の章では上の目標を実現するアルゴリズムについて解説します。

調整変数選択のアルゴリズム

d分離性の言い換え

ここではd分離性を満たす最小の変数の集合をどうやって見つけたらよいかを、計算量にも触れつつお話しようと思います。

ひとつの方法は変数の部分集合を全て列挙してその集合がd分離性を満たすかどうかを判定することです。この方法はすぐに思いつきますし、実際にこのように実装されているライブラリもあるようです。実用上はあまり問題がないかも知れませんが、変数の集合が多くなるとこの方法は非常に遅くなります。実際変数が $N$ 個だとすると計算時間が $O(2 ^ N)$ もかかるので規模が大きくなると途端に遅くなるでしょう。

アルゴリズムに詳しい人ならd分離性の定義を見たときに「ソース（処置変数）からシンク（結果変数）への全てのパスが何かしらの意味でブロックされているという定義だから、最小カットのようなアルゴリズムが使えそうだ」と思いつくかも知れません。これから述べるようにその直感は正しいのですが、最小カットを応用するためにはd分離性の定義を言い換える必要があります。それが次のモラルグラフを使った言い換えです。

定義（モラルグラフ） $G = (V, E)$ を有向非巡回グラフとする。 $G$ のモラルグラフ $G^m$ とは $V$ をノードとし、次で定義するエッジの集合をもつ無向グラフことである。 $V$ の２頂点 $v_1$ および $v_2$ に対して次のいずれかが成り立つとき $\{v_1, v_2\}$ は $G^m$ のエッジであるとする。

$v_1 \to v_2$ あるいは $v_2 \to v_1$ が $G$ のエッジである。
$G$ 内で、 $v_1$ および $v_2$ を共通の親としてもつノードが存在する。

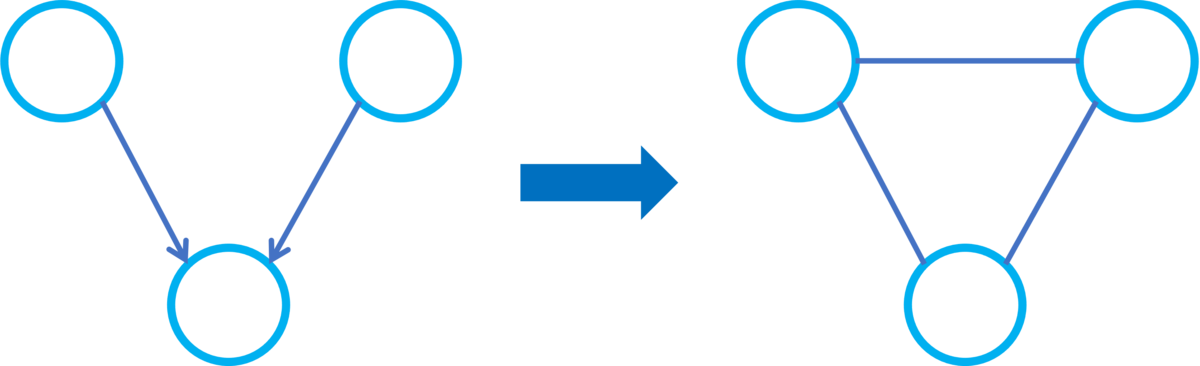
ここでモラルグラフの構築にかかる計算量を調べてみると、全てのノードのペアに対して上記２つの条件のうちいずれかを満たすかどうかをチェックするだけなので $O(N^2)$ 程度です。モラルグラフに対して次の定理が成り立つため非常に有用な概念になっています[3]。

定理（[3], Theorem 3） $G = (V, E)$ を有向非巡回グラフとする。頂点 $\{T, Y\}$ に対して $S$ を $\{T, Y\}$ の祖先の集合の部分集合であるとする。このとき $S$ が $\{T, Y\}$ をd分離することは $\{T, Y\}$ の祖先グラフのモラルグラフ $H = G_{An(T, Y)}^m$ 内で $S$ が $\{T, Y\}$ をu分離することと同値である。

この言い換えによりd分離集合を求めるためには

処置変数と結果変数の祖先グラフのモラルグラフを構築する。
モラルグラフ内でu分離する頂点集合を求める

というステップを踏めば良いことがわかりました。1.に関しては解説しましたので次は2.について解説していきます。

最小カット問題

モラルグラフ内でu分離する頂点集合を求めるというタスクは最小カット問題で解くことができます。最小カット問題とは次のような問題です。ここだけの用語ですが有向グラフ $G$ の２頂点 $u, v$ とエッジの集合 $F$ に対して $G$ から $F$ を取り除いたグラフにおいて $u$ から $v$ への有向パスが存在しないとき、 $F$ は $u, v$ をカットするということにします。

有向グラフ $G = (V, E)$ がある。また全てのエッジにはコストという値が定められているとする。始点 $S$ と終点 $G$ が定められている。始点と終点をカットする「エッジのコストの合計」の最小数はいくらか？

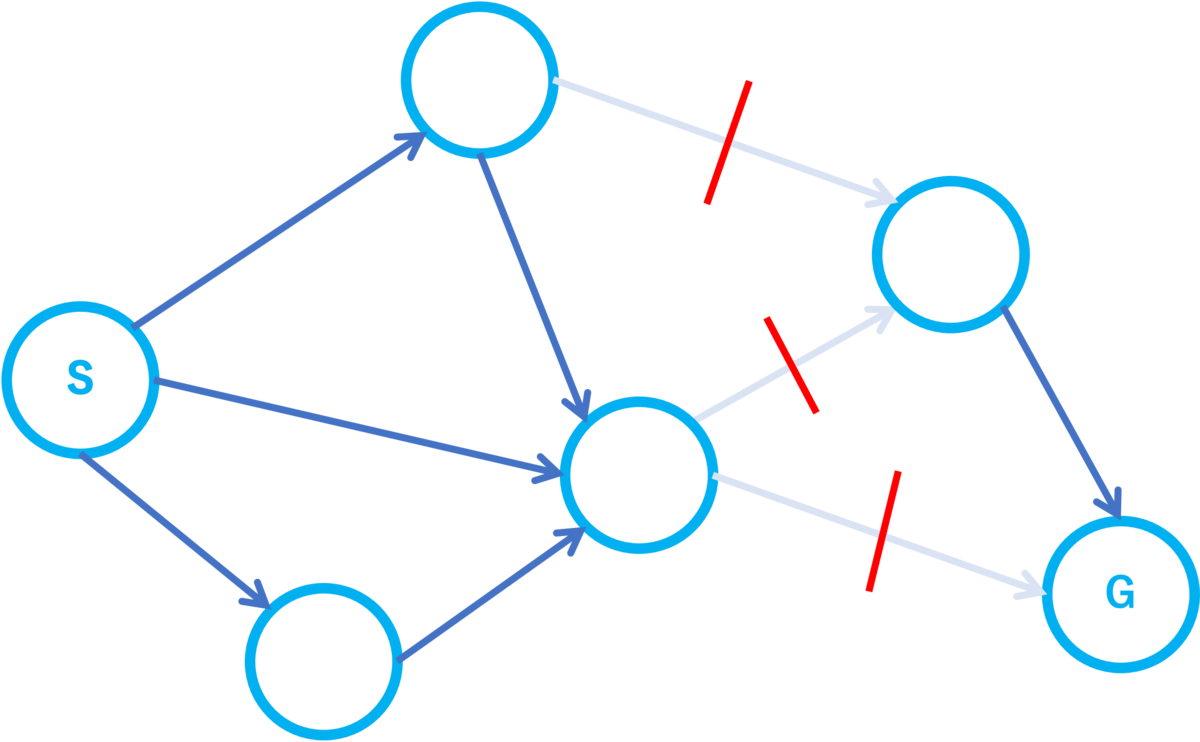
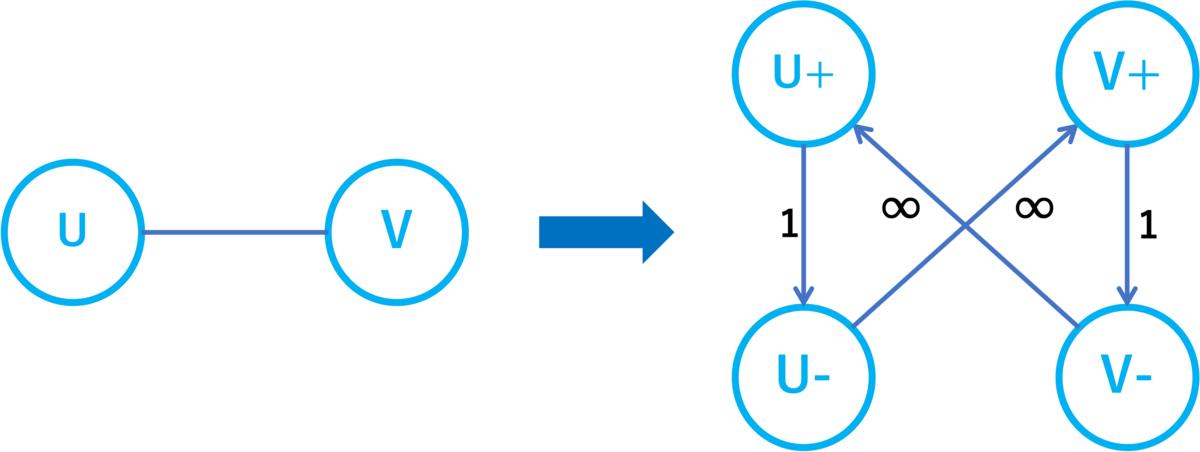
モラルグラフのu分離性に使えそうな設定の問題ですね！でも後一歩必要です。最小カット問題はエッジを除去することでパスをブロックする問題ですが、u分離性は頂点によってパスをブロックするからです。このギャップを埋めるためには次のようなグラフを考えれば良いです。

モラルグラフ $H$ のノード $u$ に対して $u_+$ および $u_-$ というノードと $u_+ \to u_-$ というエッジを作りコスト $1$ を与えます。また $u$ と $v$ をつなぐエッジが $H$ に存在する場合、 $u_- \to v_+$ および $v_- \to u_+$ というエッジを作りコスト $\infty$ を与えます。以上で作ったノードとエッジからなるグラフを $\tilde{H}$ と書きます。

$H$ と $\tilde{H}$ に対して次のことが言えます。

$H$ 内で $T$ と $Y$ をu分離するノードの集合の最小数と、 $\tilde{H}$ 内で $T_-$ と $Y_+$ の間の最小カット数は同じである。また次のように一方の問題の解から他方の問題の解への変換ができる。

$H$ において $S$ が $T, Y$ をu分離するノードの集合だとすると、 $\tilde{H}$ において $F = \{u_+ \to u_-\ | u \in S\}$ は $T_-, Y_+$ をカットする。
$\tilde{H}$ において $F$ が $T_-, Y_+$ をカットするエッジの集合だとすると、 $H$ において $S = \{u | u_+ \to u_- \in F\}$ が $T, Y$ をu分離する。

これでモラルグラフのu分離集合の求め方がわかりました！これとd分離性のモラルグラフでの言い換えと合わせると結局d分離性を満たす最小の変数集合を高速に計算できることになります！

また使ったアルゴリズムも最小カットなので適当なソルバーを使えば高速に計算できます。 $\tilde{H}$ のエッジおよびノードはそれぞれ高々 $O(N^2)$ および $O(N)$ のオーダーなのでDinicのアルゴリズムなどで最悪 $O(N^4)$ 程度の計算時間になります。愚直な方法が指数時間であることを考えると劇的な改善です！

終わりに

今回は因果推論におけるアルゴリズムの活躍についてお話ししました。筆者の乱文をここまで読んで下さった方には大変感謝いたします。以下のリストは調整変数の選択とアルゴリズムに関連する内容として興味深いですが筆者の勉強と気力が不足していて書けませんでした。またTechBlogを書く機会があってやる気に満ち溢れていたら勉強して書こうと思います。

フロントドア基準・操作変数法
optimalな調整変数の選択
mixed graphでの識別可能性
IDアルゴリズム

エクサウィザーズでは一緒に働く人を募集しています。中途、新卒両方採用していますので、興味のある方は是非ご応募ください！

参考文献

Messerli, F. H. (2012). Chocolate Consumption, Cognitive Function, and Nobel Laureates. The New England Journal of Medicine, 367, 1562-1564.
宮川雅巳. (2004). 統計的因果推論ー回帰分析の新しい枠組みー. 朝倉書店.
Tian, J., & Paz, A., & Pearl, J. (1998). Finding Minimal D-separators. Tech. Rep. R-254, Univ. of California, Los Angeles.
Acid, S., & De Campos, L. M. (2013). An algorithm for finding minimum d-separating sets in belief networks. arXiv preprint arXiv:1302.3549.

*1:選択バイアスはより広い意味で用いられることがありますがこの記事では上記の意味でのみ用います。